THE AESTHETIC AURUM

I read a book (don't panic, I read. our kind still exists) recently, Origin by Dan Brown, where the author takes this approach to entropy that made me dig deeper into the concept. Entropy, in general, meant that the universe will always tend to decline into a disordered state. That is, everything that happens in the universe happens with an objective to attain the disordered state. But, when we give our eyes some strain and brain some food, all we can see is an immaculate symmetry in the big guns like the galaxies, orbits and the smaller entities, yet not any less magnificent, as flowers, radiant trees and all in all the most complex beings, humans. But the argument of entropy seems to be a little derailing because of the seemingly obvious order in the universe. Does that mean the law doesn't hold true?

This Image cracked me up. find the source Here.

That's what was discussed in the book when Brown says that the order is a value addition for the disorder. It does hold true, according to him and also subjectively by me, the order exists to help the disorder spread faster. The universe develops itself into clusters of stars to develop into galaxies with a seemingly improbable and recurring pattern, where there are just a handful of patterns, in which the galaxies can be studied. When these kinds of patterns are formed, the objective behind it is to spend more energy through efficient wastage. Let's consider if the cosmic dust stayed as dust, while never forming any sizable entities the probability that the atoms interact with each other to give out energy is much less as the space among the particles becomes wider and unoriented. Therefore the number of collisions that occur are far lesser than the structured cosmic dust.

Img Source: https://briankoberlein.com/2014/10/08/learning-curve/

Same goes with the trees that branch out to give a symmetric pattern like a solid cloud on a candlestick, the branches which branch out from the root in a sequence of 0,1,1,2,3,5,8,... and flowers that show the concentric circles. The order that is created to satisfy the disorder is so beautiful and mathematical that it "almost" feels like someone did it on purpose. But, All the mysteries are mystical before science proved them otherwise. All the patterns have a reason to exist because they help the universe to dispel energy more efficiently. Anyway, let's leave this randomness (though impossible) and get into the patterns that make our world look beautiful.


The Ratio is golden:


Let's get mathematical for a single moment. Draw a straight line and divide it into two parts A and B(let's consider A the longer side)such the ratio of total line to the longest part(A+B/A) is equal to the ratio of A and B (i.e., A/B).


=> A+B/A = A/B

 

If we calculate, by solving, the above quadratic equation the amount of A and B needed to achieve this can be approximated as

A = (1.618) B

Therefore the golden ratio is approximated (Approximated because it is irrational) is 1.618.

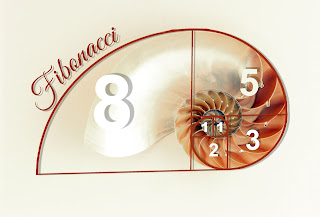
Though not so relevant, but breathtakingly coincidental is the Fibonacci series. Fibonacci series is a series of numbers that are continued by the addition of two preceding numbers

0,1,1,2,3,5,8,11,19,.......etc

When we consider the ratio of two consecutive numbers in this series they tread very close to the golden ratio. A very weird coincidence and it gets weirder down these lines.

"TOO MUCH MATH", Okay, lets tone it down a little bit and explore the part where this math explains the wonders of the world.

Everybody Loves Flowers:

Flowers are made very beautiful to attract the insects to take a peek at these structures and mainly carry the pollen. This beauty happens to be very enticing to us too. The petals of the flowers are also strategically one of the Fibonacci numbers, at least most of them. For Instance, the flowers may contain 13,21,34 or some other Fibonacci number. When the flower viewed from the top can be imagined to have these concentric circles(circles with the same center point), these circles are so placed that the distance from the center to each of the concentric circle follows Fibonacci series. It is just really weird to stumble upon a red rose and that to have better math ability than inferior humans. So what would be the reason for this to happen? It happens to be this way because it allows the flower to optimize its exposure to the sunlight and also, maybe, to say that we are dumb. 

It is hard to ignore the golden ratio once you know the gravity of its presence in nature. All you can ever do, after knowing about it, is to check whether the structure follows the golden ratio.

Let me give some Illustrations of the golden ratio:

  

1. The above geometry is one of the many spectacular designs that nature exhibits. It may sound a little fishy but let me give a fishy example.

The Sea neighbor of fish, mollusk, has this unique structural design pattern on its back which seems familiar, now that we know the Fibonacci. Numerous mollusks carry this kind of a shell.

2. The elegant chrysanthemum shows the positioning of the petals in circles from the center flowing outwards with the relative distance being a Fibonacci series.

3. The buttercup flower where the petals can be counted to a Fibonacci number.

Img Source: https://botanicamathematica.wordpress.com/2014/04/01/fibonacci-tree/

4. The tree in its mathematical glory.

5. And, of course, the human face. If you are interested to know more there are plenty of articles to read from(for a starter).


AND MORE AND MORE AND MORE.


These are just a few famous examples that I've presented but be aware that there are many other patterns too and they run deep into our universe. I cannot give out all the details, else I would have to write a tome.

Maybe these patterns in nature are like physics. we know the universe follows the laws of physics not because we proved the laws. We have physics because the universe acts that way, not that physics made the universe to act the way it does. Universe gave us the laws and not the other way around. Patterns, in the same way, are always universal and are found everywhere we see them. Similarly, this is also the other way around. patterns are not due to mathematics, instead, mathematics is due to patterns.